Use the cosine calculator to find the cos value based on a given degree or radian. Instead of numbers in radians, you can also enter radians in π combinations.
What is cosine?
In a right triangle, the ratio of the side adjacent to the angle to the hypotenuse is called the cosine. It is called cos for short. Like sine, cosine is also one of the three major functions in trigonometric functions, the other is tangent.
The cosine formula is
cos(θ) = adjacenthypotenuse
For instance, there is a right triangle as follows
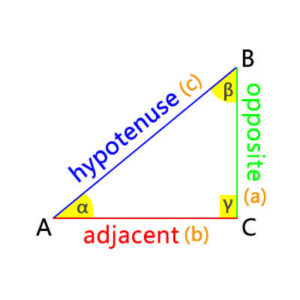 In this right triangle, the three angles are α, β and γ, where γ is the right angle. The three sides are a, b, and c, where c is the hypotenuse. Therefore, the cosines of these three angles are
In this right triangle, the three angles are α, β and γ, where γ is the right angle. The three sides are a, b, and c, where c is the hypotenuse. Therefore, the cosines of these three angles are
cos(α) = adjacenthypotenuse = bc
cos(β) = oppositehypotenuse= ac
cos(γ) = 0
Why is the cosine of a right angle equal to 0?
The first thing to be clear is that cosine calculates ratios based on right triangles. When two right angles appear in a right triangle (90°, 90°, 0), then the triangle becomes a line segment. Therefore, the length of the adjacent side of a right angle is 0. So, the cosine of 90° is 0.
How to calculate cosine?
There are two ways to calculate the cosine of an angle.
The first method is that the adjacent and hypotenuse lengths are known.
For example, in a right triangle, the length of the adjacent side of angle α is 3, and the length of the hypotenuse is 5. What is the cosine of angle α?
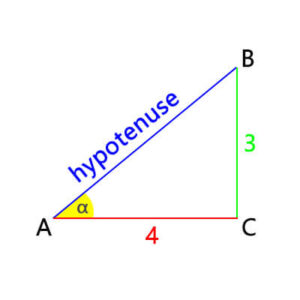
cos(α) = adjacenthypotenuse = 45
Another way is to know the degrees or radians of the angle. At this time, you can use the cosine calculator we provided above to calculate it. Alternatively, find the cosine in degrees or radians from the cosine table (provided below). The fatal flaw of the cosine table is that it cannot list all degrees or radians. We list some commonly used cosine degrees or radians.
| Degrees | Radians | Cos |
| 0° | 0 | 1 |
| 5° | π36 | 0.9961947 |
| 10° | π18 | 0.98480775 |
| 15° | π12 | 0.96592583 |
| 20° | π9 | 0.93969262 |
| 25° | 5π36 | 0.90630779 |
| 30° | π6 | 0.8660254 |
| 35° | 7π36 | 0.81915204 |
| 40° | 2π9 | 0.76604444 |
| 45° | π4 | 0.70710678 |
| 50° | 5π18 | 0.64278761 |
| 55° | 11π36 | 0.57357644 |
| 60° | π3 | 0.5 |
| 65° | 13π36 | 0.42261826 |
| 70° | 7π18 | 0.34202014 |
| 75° | 5π12 | 0.25881905 |
| 80° | 4π9 | 0.17364818 |
| 85° | 17π36 | 0.08715574 |
| 90° | π2 | 0 |
| 95° | 19π36 | -0.08715574 |
| 100° | 5π9 | -0.17364818 |
| 105° | 7π12 | -0.25881905 |
| 110° | 11π18 | -0.34202014 |
| 115° | 23π36 | -0.42261826 |
| 120° | 2π3 | -0.5 |
| 125° | 25π36 | -0.57357644 |
| 130° | 13π18 | -0.64278761 |
| 135° | 3π4 | -0.70710678 |
| 140° | 7π9 | -0.76604444 |
| 145° | 29π36 | -0.81915204 |
| 150° | 5π6 | -0.8660254 |
| 155° | 31π36 | -0.90630779 |
| 160° | 8π9 | -0.93969262 |
| 165° | 11π12 | -0.96592583 |
| 170° | 17π18 | -0.98480775 |
| 175° | 35π36 | -0.9961947 |
| 180° | π | -1 |
| 185° | 37π36 | -0.9961947 |
| 190° | 19π18 | -0.98480775 |
| 195° | 13π12 | -0.96592583 |
| 200° | 10π9 | -0.93969262 |
| 205° | 41π36 | -0.90630779 |
| 210° | 7π6 | -0.8660254 |
| 215° | 43π36 | -0.81915204 |
| 220° | 11π9 | -0.76604444 |
| 225° | 5π4 | -0.70710678 |
| 230° | 23π18 | -0.64278761 |
| 235° | 47π36 | -0.57357644 |
| 240° | 4π3 | -0.5 |
| 245° | 49π36 | -0.42261826 |
| 250° | 25π18 | -0.34202014 |
| 255° | 17π12 | -0.25881905 |
| 260° | 13π9 | -0.17364818 |
| 265° | 53π36 | -0.08715574 |
| 270° | 3π2 | 0 |
| 275° | 55π36 | 0.08715574 |
| 280° | 14π9 | 0.17364818 |
| 285° | 19π12 | 0.25881905 |
| 290° | 29π18 | 0.34202014 |
| 295° | 59π36 | 0.42261826 |
| 300° | 5π3 | 0.5 |
| 305° | 61π36 | 0.57357644 |
| 310° | 31π18 | 0.64278761 |
| 315° | 7π4 | 0.70710678 |
| 320° | 16π9 | 0.76604444 |
| 325° | 65π36 | 0.81915204 |
| 330° | 11π6 | 0.8660254 |
| 335° | 67π36 | 0.90630779 |
| 340° | 17π9 | 0.93969262 |
| 345° | 23π12 | 0.96592583 |
| 350° | 35π18 | 0.98480775 |
| 355° | 71π36 | 0.9961947 |
| 360° | 2π | 1 |
Cosine graph and range
If you connect the cosine values of each degree, you can get a smooth curve, which is also called a cosine graph.
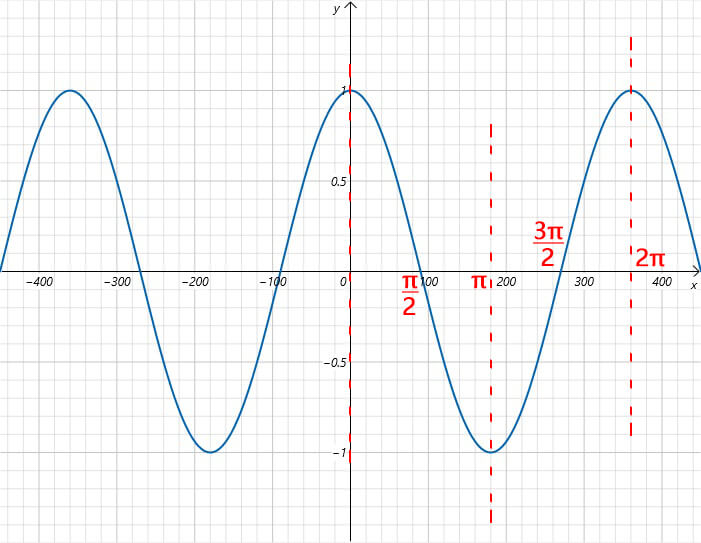 It can be seen from the curve that the value range of cosine is between -1 and 1. The axis of symmetry of the cosine is kπ (k is an integer). The period is the same as the sine, which is 2π.
It can be seen from the curve that the value range of cosine is between -1 and 1. The axis of symmetry of the cosine is kπ (k is an integer). The period is the same as the sine, which is 2π.
cos(θ) = cos (θ + n * 360°) = cos (θ + n * 2π)
Also, the graph is left-right symmetrical, therefore, the cosine function is an even function.
In addition, when the angle is in different quadrants, the positive and negative values of the cosine are different. Positive in the first and fourth quadrants, negative in the second and third quadrants.
| Quadrant | Degrees | Radians | Sign | Cos Values | Monotonicity |
| 1 | 0° < θ < 90° | 0 < θ < π2 | + | 0 < cos(θ) < 1 | Decreasing |
| 2 | 90° < θ < 180° | π2 < θ < π | – | -1 < cos(θ) < 0 | Decreasing |
| 3 | 180° < θ < 270° | π < θ < 3π2 | – | -1 < cos(θ) < 0 | Ascending |
| 4 | 270° < θ < 360° | 3π2 < θ < 2π | + | 0 < cos(θ) < 1 | Ascending |
Other calculations for cosine
There are 3 calculations closely related to cosine.
1. Cosine derivative
The derivative of the cosine function is the negative sine function.
cos'(θ) = -sin(θ) = –oppositehypotenuse
2. Inverse cosine
The inverse of cosine is arccosine, which is used to find the angle from the cosine value. It can be represented by cos-1 or arccos.
cos(90°) = 0
cos-1(0) = arccos (0) = 90°
3. Reciprocal cosine
The reciprocal of cosine is secant, which is also a type of trigonometric function. In a right triangle, the secant of an acute angle is equal to the ratio of its hypotenuse to its adjacent side. The abbreviation is sec.
1cos(θ) = sec(θ)
How to use this cosine calculator
There are two steps to using the cosine calculator. In the first step, enter a value. In the second step, choose the type, degrees or radians. Finally, click Calculate to get the cosine value. This cosine calculator supports the input of π, and the combination of π, such as 3π/2, 5π, etc. Fill in according to the actual situation. Please press the reset button before running a new calculation.
FAQS
- Q: Why do you need a cosine calculator?A: The calculation of cosine is troublesome, especially for some degrees or radians that are not commonly used, it is impossible for you to calculate them by hand. Therefore, you need a cosine calculator.
- Q: How to enter pi (π)?A: There are two ways, one is to input or copy and paste π, and the other is to enter pi directly.
- Q: Can I enter decimals or fractions?A: Yes, it’s OK. The symbol for fractions is /, such as 2/3, π/4.
- Q: What is the relationship between cosine and sine?A: The derivative of sine is cosine. The derivative of cosine is the negative sine. The sum of squares of sine and cosine equals 1.
sin'(θ) = cos(θ)
cos'(θ) = -sin(θ)
sin2(θ) + cos2(θ) = 1
- Q: Can cosine be negative?A: Yes, it is possible.
- Q: Can cosine be greater than 1?A: No, cosine cannot be greater than 1. Cosine ranges from -1 to 1.
Conclusion
Like sine, cosine is a very important trigonometric function. You can remember some commonly used cosine values, but it is absolutely impossible to remember all cosine values. Therefore, you should desperately need a cosine calculator to help you, that’s why our cosine calculator exists. Hurry to try it!
Latest Calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Trigonometric Functions
Arccsc Calculator – Find the Exact Value of Inverse Cosecant
Arcsec Calculator – Find the Exact Value of Inverse Secant
Arccot Calculator – Find the Exact Value of Inverse Cotangent
Arctan Calculator – Find the Exact Value of Inverse Tangent
Inverse Cosine Calculator – Find The Exact Value of Arccos
Inverse Sine Calculator – Find The Exact Value of Arcsin
Inverse Trigonometric Functions Calculator
Trigonometric Functions Conversion Calculator
Trig Calculator – Find 6 Trigonometric Functions by Angles or Sides