Welcome to the Cosecant Calculator. This calculator can be used to calculate the cosecant of any angle. The angle can be expressed in degrees or radians.
What is cosecant?
In a right triangle, the ratio of the hypotenuse to the opposite side of an acute angle is called the cosecant. Cosecant is also one of the trigonometric functions. The cosecant abbreviation is csc.
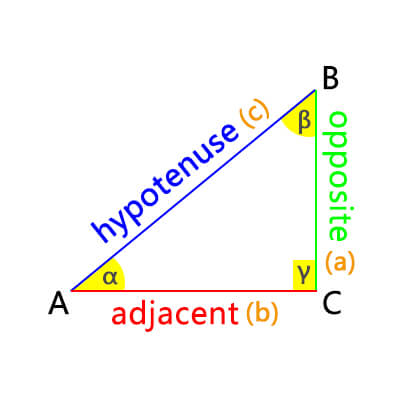 The cosecant formula is
The cosecant formula is
csc(θ) = hypotenuseopposite
Review another commonly used trigonometric function: sine. The sine is defined as the ratio of the opposite side of the acute angle to the hypotenuse in a right triangle. Just the opposite of cosecant. Therefore, the relationship between cosecant and sine is reciprocal.
How to calculate cosecant?
As with other trigonometric functions, there are two methods.
When the side lengths are known.
This case is relatively simple. Substitute the relevant values into the cosecant formula. It should be noted that a right triangle needs to give at least 2 side lengths. If it is not the hypotenuse and the opposite side, you need to use the Pythagorean theorem to calculate the other side.
For example, the length of the hypotenuse of a right triangle is 5, and the length of the side adjacent to angle α is 3. What is the cosecant of angle α?
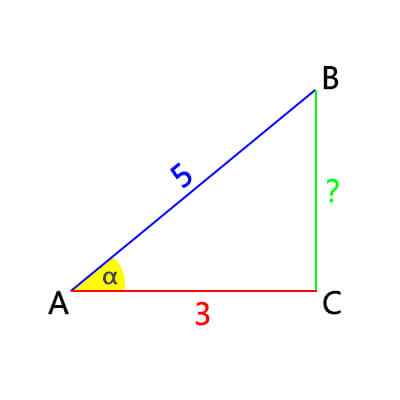 First, find the opposite side.
First, find the opposite side.
opposite2 + adjacent2 = hypotenuse2
opposite2 + 32 = 52
opposite2 + 9 = 25
opposite2 = 16
opposite = 4
Second, substitute the opposite and hypotenuse into the formula.
csc(α) = hypotenuseopposite = 54
So, the cosecant of angle α is 54.
When the angle degree is known.
In this case, the calculation is usually done with the help of a cosecant calculator. Because the cosecant of degrees is difficult to calculate directly by hand. That’s why we developed this cosecant calculator!
If you don’t have a cosecant calculator, you can use the cosecant table, and find the corresponding cosecant according to degrees or radians.
| Degrees | Radians | Csc |
| 5° | π36 | 11.47371325 |
| 10° | π18 | 5.75877048 |
| 15° | π12 | 3.86370331 |
| 20° | π9 | 2.9238044 |
| 25° | 5π36 | 2.36620158 |
| 30° | π6 | 2 |
| 35° | 7π36 | 1.7434468 |
| 40° | 2π9 | 1.55572383 |
| 45° | π4 | 1.41421356 |
| 50° | 5π18 | 1.30540729 |
| 55° | 11π36 | 1.22077459 |
| 60° | π3 | 1.15470054 |
| 65° | 13π36 | 1.10337792 |
| 70° | 7π18 | 1.06417777 |
| 75° | 5π12 | 1.03527618 |
| 80° | 4π9 | 1.01542661 |
| 85° | 17π36 | 1.00381984 |
| 90° | π2 | 1 |
| 95° | 19π36 | 1.00381984 |
| 100° | 5π9 | 1.01542661 |
| 105° | 7π12 | 1.03527618 |
| 110° | 11π18 | 1.06417777 |
| 115° | 23π36 | 1.10337792 |
| 120° | 2π3 | 1.15470054 |
| 125° | 25π36 | 1.22077459 |
| 130° | 13π18 | 1.30540729 |
| 135° | 3π4 | 1.41421356 |
| 140° | 7π9 | 1.55572383 |
| 145° | 29π36 | 1.7434468 |
| 150° | 5π6 | 2 |
| 155° | 31π36 | 2.36620158 |
| 160° | 8π9 | 2.9238044 |
| 165° | 11π12 | 3.86370331 |
| 170° | 17π18 | 5.75877048 |
| 175° | 35π36 | 11.47371325 |
| 185° | 37π36 | -11.47371325 |
| 190° | 19π18 | -5.75877048 |
| 195° | 13π12 | -3.86370331 |
| 200° | 10π9 | -2.9238044 |
| 205° | 41π36 | -2.36620158 |
| 210° | 7π6 | -2 |
| 215° | 43π36 | -1.7434468 |
| 220° | 11π9 | -1.55572383 |
| 225° | 5π4 | -1.41421356 |
| 230° | 23π18 | -1.30540729 |
| 235° | 47π36 | -1.22077459 |
| 240° | 4π3 | -1.15470054 |
| 245° | 49π36 | -1.10337792 |
| 250° | 25π18 | -1.06417777 |
| 255° | 17π12 | -1.03527618 |
| 260° | 13π9 | -1.01542661 |
| 265° | 53π36 | -1.00381984 |
| 270° | 3π2 | -1 |
| 275° | 55π36 | -1.00381984 |
| 280° | 14π9 | -1.01542661 |
| 285° | 19π12 | -1.03527618 |
| 290° | 29π18 | -1.06417777 |
| 295° | 59π36 | -1.10337792 |
| 300° | 5π3 | -1.15470054 |
| 305° | 61π36 | -1.22077459 |
| 310° | 31π18 | -1.30540729 |
| 315° | 7π4 | -1.41421356 |
| 320° | 16π9 | -1.55572383 |
| 325° | 65π36 | -1.7434468 |
| 330° | 11π6 | -2 |
| 335° | 67π36 | -2.36620158 |
| 340° | 17π9 | -2.9238044 |
| 345° | 23π12 | -3.86370331 |
| 350° | 35π18 | -5.75877048 |
| 355° | 71π36 | -11.47371325 |
Cosecant graph and range
Now, we will combine the cosecant curve to summarize the properties of the cosecant.
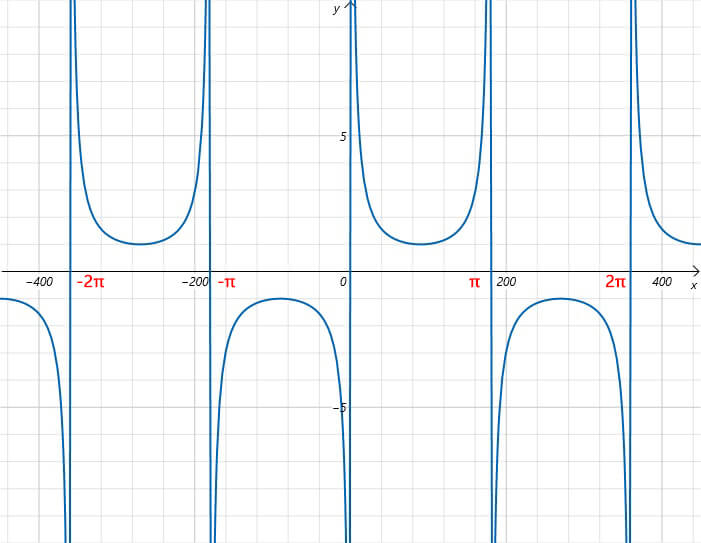
- Domain – The domain of the cosecant function is all values except kπ (k is an integer).
- Range – The cosecant range is the same as the secant, the absolute value of the cosecant is greater than or equal to 1.
- Period – The smallest period of cosecant is 2π. csc(θ) = csc(θ + 2π)
- Odd function – Since csc(θ) = -csc(-θ), cosecant is an odd function.
Furthermore, in different quadrants of the coordinate axis, the cosecant ranges are also different. Cosecant comparisons for the four quadrants are listed below.
| Quadrant | Degrees | Radians | Sign | Csc Values | Monotonicity |
| 1 | 0° < θ < 90° | 0 < θ < π2 | + | csc(θ) > 1 | Decreasing |
| 2 | 90° < θ < 180° | π2 < θ < π | + | csc(θ) > 1 | Ascending |
| 3 | 180° < θ < 270° | π < θ < 3π2 | – | csc(θ) < -1 | Ascending |
| 4 | 270° < θ < 360° | 3π2 < θ < 2π | – | csc(θ) < -1 | Decreasing |
Other calculations for cosecant
1. Cosecant derivative
The derivative of cosecant is equal to negative cotangent times cosecant. Its derivation process is as follows
(csc(θ))’
= (1sin(θ))’
= -sin(θ)’sin2(θ)
= -cos(θ)sin2(θ)
= -cot(θ) * 1sin(θ)
= -cot(θ) * csc(θ)
2. Inverse cosecant
The inverse of cosecant is arccosecant, denoted as arccsc, or csc-1. It is a type of inverse trigonometric function.
csc(90°) = 1
csc-1(1) = arccsc (1) = 90°
3. Reciprocal cosecant
The reciprocal of cosecant is sine, which is equal to the ratio of its opposite side to its hypotenuse side. The abbreviation is sin.
1csc(θ) = sin(θ)
How to use this cosecant calculator
The cosecant calculator is very easy to use, three steps:
First, enter degrees or radians. Such as, 45, π, 2π/5 and so on. If you don’t know how to enter π, just type pi instead.
Second, choose the type, degrees or radians.
Finally, click Calculate button to get the cosecant answer, or click Reset button to start a new calculation.
FAQS
- Q: What is cosecant of pi?A: The cosecant of pi does not exist.
- Q: What is cosecant of 45 degrees?A: The cosecant of 45° is 1.41421356. The right triangle at this time is an isosceles right triangle. Therefore, the cosecant of 45° is equal to the secant of 45°.
- Q: Can cosecant equal zero?A: No. The range of cosecant is less than or equal to -1, or greater than or equal to 1.
- Q: Is cosecant the opposite of sine?A: Yes, they are reciprocal.
- Q: What is the difference between cosecant and arcsine?A: Many people confuse the two because cosecant is the reciprocal of sine, so that people mistakenly think that cosecant is arcsine. Actually, no. Cosecant is one of the trigonometric functions while arcsine is one of the inverse trigonometric functions. Cosecant is to calculate the ratio of the hypotenuse to the opposite side, while arcsine is to obtain an angle based on the ratio. Their concepts and functions are completely different.
- Q: Can I enter decimals or fractions? How to enter?A: Yes, sure. Decimals are entered directly. When entering fractions, the numerator and denominator are divided by /, such as 1/2, 3π/4 and so on.
Latest Calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Trigonometric Functions
Arccsc Calculator – Find the Exact Value of Inverse Cosecant
Arcsec Calculator – Find the Exact Value of Inverse Secant
Arccot Calculator – Find the Exact Value of Inverse Cotangent
Arctan Calculator – Find the Exact Value of Inverse Tangent
Inverse Cosine Calculator – Find The Exact Value of Arccos
Inverse Sine Calculator – Find The Exact Value of Arcsin
Inverse Trigonometric Functions Calculator
Trigonometric Functions Conversion Calculator
Trig Calculator – Find 6 Trigonometric Functions by Angles or Sides