Consecutive Calculator: Discover Consecutive Integers Based on Given Sum

Welcome to the Consecutive Calculator, a specialized calculator designed to pinpoint consecutive integers, whether they’re odd, even, or a mix, that add up to a specific sum. This is the reverse calculation of the sum of consecutive integers.

Let’s start with an example: find three consecutive integers whose sum is 75.

First of all, suppose the first integer of these three consecutive integers is n, then the second integer should be n + 1, and the third integer is n + 2. Thus, the equation is as follows:

n + (n + 1) + (n + 2) = 75

The next steps are much simpler, just solve this equation:

n + (n + 1) + (n + 2) = 75

n + n + 1 + n + 2 = 75

3 * n + 1 + 2 = 75

3 * n + 3 = 75

3 * n = 75-3

3 * n = 72

n = 72 / 3

n = 24

Therefore, the calculated value of n is 24, that is, the first integer is 24, so the second integer is 24 + 1 = 25, the third integer is 24 + 2 = 26

Let us verify that 24 + 25 + 26 = 75. It fully meets the requirements.

Let’s look at another example: the sum of five consecutive integers is 120 find the integers.

Similarly, we assume that the first integer is n, then the consecutive integers from 2 to 5 are: n + 1, n + 2, n + 3, n + 4. The equation is as follows:

n + (n + 1) + (n + 2) + (n + 3) + (n + 4) = 120

solve this equation:

n + (n + 1) + (n + 2) + (n + 3) + (n + 4) = 120

n + n + 1 + n + 2 + n + 3 + n + 4 = 120

5 * n + 1 + 2 + 3 + 4 = 120

5 * n + 10 = 120

5 * n = 120 -10

5 * n = 110

n = 110 / 5

n = 22

The answer comes out, the first integer is 22, the 5 consecutive integers are: 22, 23, 24, 25, 26.

Verify it: 22 + 23 + 24 + 25 + 26 = 120. The answer is correct.

In the process of answering, did you find a characteristic? That’s right, 1 + 2 + 3 + 4 is the sum of consecutive integers, so, you can replace them with the formula for the sum of consecutive integers:

4 * (1 + 4) / 2 = 10

Replace in equation

n + (n + 1) + (n + 2) + (n + 3) + (n + 4) = 120

5 * n + 1 + 2 + 3 + 4 = 120

5 * n + 4 * (1 + 4) / 2 = 120

Therefore, assuming that the number of consecutive integers we require is M and the sum is S, then the above equation can be replaced by:

M * n + (M – 1) * (1 + M – 1) / 2 = S

M * n + (M – 1) * M / 2 = S

M * n = S – (M – 1) * M / 2

So, we get the formula for the first integer in consecutive integers whose sum is S:

First(n) = (S – (M -1) * M / 2) / M = S / M – (M – 1) / 2

n is the first integer of the M consecutive integers we require. Note that n must be an integer when calculated. Positive or negative integers are acceptable, but they cannot be decimals or fractions.

Verify that the sum of 5 consecutive integers is 505. Use the formula to calculate:

First(n) = 505 / 5 – (5 – 1) / 2 = 101 – (5 – 1) / 2 = 101 – 4 / 2 = 101 – 2 = 99

These 5 consecutive integers are: 99, 100, 101, 102, 103. Their sum also happens to be 505, which is completely correct.

After discussing consecutive integers, let’s discuss consecutive even integers: the sum of 3 consecutive even numbers is 234 find the numbers?

We know that an even number is an integer that can be divisible by 2. Assuming that the first even integer is 2 * n, so the second consecutive even integer is 2 * n + 2, the third even integer is 2 * n + 4, n is an integer. The equation is:

2 * n + (2 * n + 2)  +  (2 * n + 4) = 234

Calculate this equation

2 * n + (2 * n + 2) + (2 * n + 4) = 234

2 * n + 2 * n + 2 + 2 * n + 4 = 234

6 * n + 2 + 4 = 234

6 * n + 6 = 234

6 * n = 234 – 6

6 * n = 228

n = 228 / 6

n = 38

Therefore, the three consecutive even integers are: 2 * 38 = 76, 2 * 38 + 2 = 78, 2 * 38 + 4 = 80.

Verification: 76 + 78 + 80 = 234, which meets the conditions.

As above, we regard 2 + 4 in the calculation process as 0 + 2 + 4, which is a continuous even integers. Then, replace this part with the formula of continuous integers sum:

6 * n + 0 + 2 + 4 = 234

6 * n + 3 * (0 + 4) / 2 = 234

3 * 2 * n + 3 * ( 0 + 4 ) / 2 = 234

Among them, the number 4 is the third number with the first number of the arithmetic sequence being 0 and the common difference is 2. So, this equation can be transformed into:

3 * 2 * n + 3 * (0 + 4) / 2 = 234

3 * 2 * n + 3 * (0 + (3 – 1) * 2) / 2=234

3 * 2 * n + 3 * ( (3 – 1) * 2) / 2 = 234

3 * 2 * n + 3 * (3-1) = 234

Assuming that the number of consecutive even integers is M and the sum is S, the above equation can be replaced by:

M * 2 * n + M * (M – 1) = S

Now, we can get the formula for the first even integer among consecutive even integers whose sum is S:

First(e) = (S – M * (M – 1)) / M = S / M – M + 1

Pay special attention that if the calculated result is an odd integer, it means that not found M consecutive even integers whose sum is S. Of course, if the result is a decimal or fraction, it is also not acceptable.

The above example: the sum of 3 consecutive even numbers is 234 find the numbers? Use this formula to calculate:

First(e) = 234 / 3 – 3 + 1 = 78 – 3 + 1 = 76

It is exactly the same as the result of the above non-formula calculation.

Let’s look at another example: the sum of 5 consecutive even integers is 120. Using the formula, the first even integer should be:

First(e) = 120 / 5 – 5 + 1 = 24 – 5 + 1 = 19 + 1 = 20

Thus, the 5 consecutive even integers are: 20, 22, 24, 26, 28

Verification: 20 + 22 + 24 + 26 + 28 = 120, the answer is correct!

So

The sum of 5 consecutive even integers is 120, the smallest even integer is 20.

The sum of 5 consecutive even integers is 120, the largest even integer is 28.

Similar to even integers, the sum of M consecutive odd integers is S, the formula for the first odd integer is:

First(o) = S / M – M + 1

The formula is the same as continuous even integers, but it is worth noting that the calculated result must be an odd number. If it is an even number, a decimal number or a fraction, it means that there are no such M consecutive odd integers whose sum is equal to S.

For example, the sum of 3 consecutive odd integers is 30, find these odd integers. According to the above formula

First(o) = 30 / 3 – 3 + 1 = 10 – 3 + 1 = 8

8 is an even integer, so there are no three consecutive odd integers that sum to 30.

For another example, the sum of 5 consecutive odd integers is 135. The first odd integer is:

First(o) = 135 / 5 – 5 + 1 = 27 – 5 + 1 = 23

Therefore, these 5 consecutive odd integers are: 23, 25, 27, 29, 31

Recheck: 23 + 25 + 27 + 29 + 31 = 135. Correct answer.

The sum of 5 consecutive even integers is 135, the smallest one is 23, the largest one is 31.

The consecutive integers, consecutive even integers, and consecutive odd integers are discussed above, and the corresponding formulas are obtained. You can manually calculate according to the formula, or you can use our calculator directly. Of course, our calculator can help you save many steps, let you get the answer directly, which is convenient and fast!

Well, through the above introduction, you should not wait to know how to use our consecutive integers calculator. Don’t worry, our calculator is very easy to use. The detailed steps are described below:

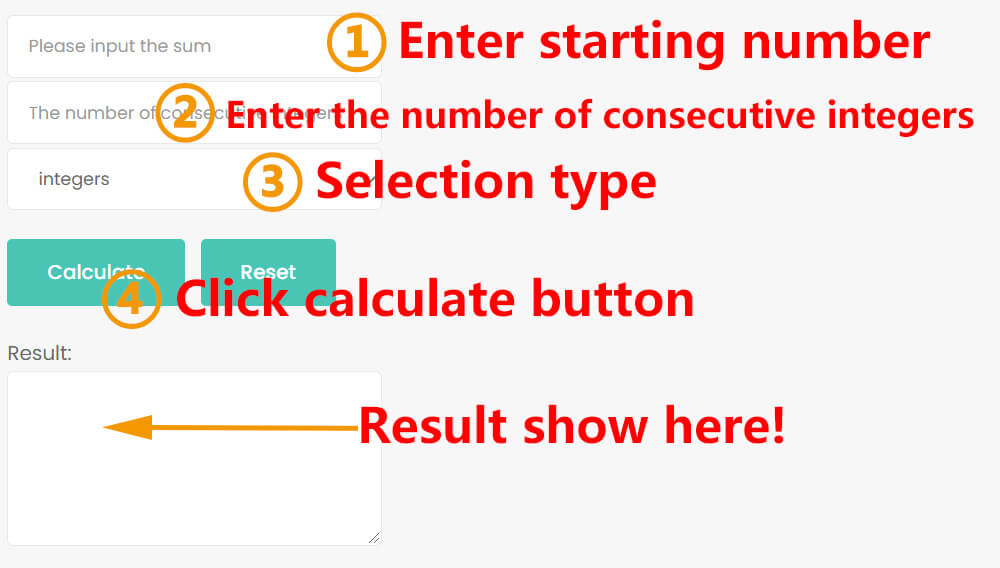It’s very simple, just 4 steps, if you still don’t understand, look at the examples below.

Example 1: The sum of 3 consecutive integers is 75.

First, enter 75 into the first input box. Second, enter 3 in the second input box. Then click Calculate.

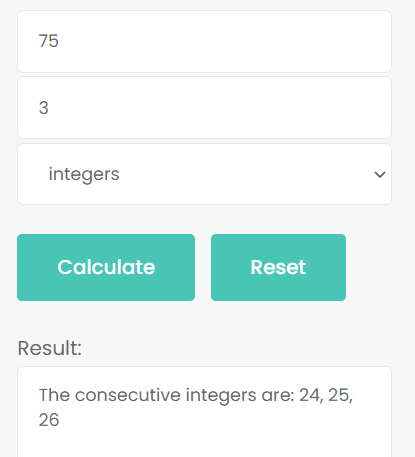Verify: 24 + 25 + 26 = 75

Example 2: The sum of 5 consecutive even numbers is 100.

Enter the number 100 in the first input box, enter the number 5 in the second input box, then select the even integers, finally click Calculate.

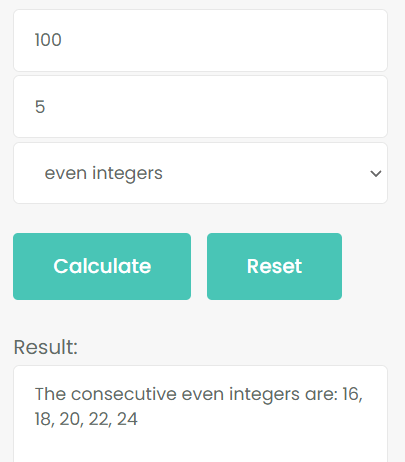Verify: 16 + 18 + 20 + 22 + 24 = 100

Example 3: The sum of 5 consecutive odd numbers is 145.

First, enter the number 145 into the first input box, then enter 5 into the second input box. Third, select the odd integers type. Fourth, click Calculate.

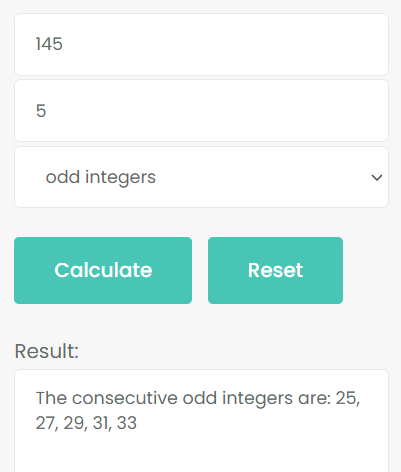Verify: 25 + 27 + 29 + 31 + 33 = 145

Okay, let’s recall the three important formulas on this page.

Given the sum S, find M consecutive integers, the formula of the first integer is:

First(n) = S / M – (M – 1) / 2

Given the sum S, find M consecutive even integers, the formula for the first even integer is:

First(e) = S / M – M + 1

Given the sum S, find M consecutive odd integers, the formula for the first odd integer is:

First(o) = S / M – M + 1

With these three formulas, you should be able to easily solve the problem of finding consecutive integers, even integers or odd integers. Of course, there is another method, which is to use our free online continuous integer calculation, which is very simple and convenient. We sincerely look forward to your use!