Circular Segment Radius Calculator

Unveiling 5 Methods and Formulas

The Circular Segment Radius Calculator is a handy tool designed to unravel the mysteries of circular segmentradius. Whether you’re working with arcs, chords, or heights, this calculator is your key to finding the radius with ease.

Circular Segment Radius Calculator

Calculate Reset

Definition

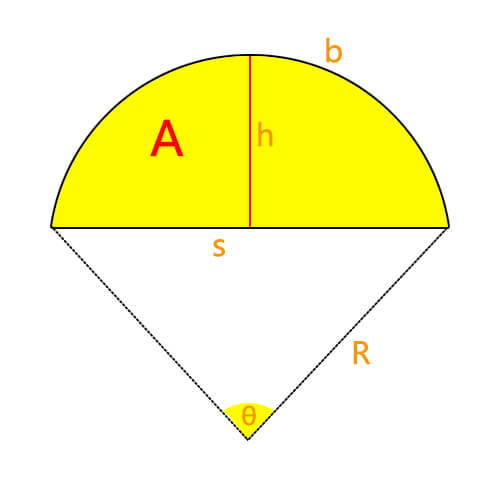A circular segment is a region enclosed by a chord and the arc of a circle. The Circular Segment Radius is the distance from the center of the circle to the arc (R in the picture), defining the curvature of this segmented area.

How to Calculate the Radius of a Circular Segment

1. Arc Length Method

To calculate the radius (R) of a circular segment when the arc length (b) and central angel (θ) are given, the formula is:

R = 180°* b/(θ * π)

Example: If the arc length (b) is 8 units and the central angle (θ) is 60 degrees, the radius is:

R = 180°* b/(θ * π) = 180°* 8 /(60° * π) = 7.639 units

2. Chord Length Method

If the chord length (s) and the central angle (θ) are known, the formula to find the radiusof a circular segmentbecomes:

R = s/(2 * sin(θ/2))

Example: For a chord length (s) of 10 units and a central angle (θ) of 45 degrees, the radius of the circular segment is

R = s/(2 * sin(θ/2)) = 10/(2*sin(45°/2)) = 13.066 units

3. Height Method

When the height of the circular segment (h) and the central angle (θ) are given, the formula is:

R = h/(1 – cos(θ/2))

Example: With a height (h) of 6 units and a central angle (θ) of 90 degrees, the radius is:

R = h/(1 – cos(θ/2)) = 6/(1 – cos(90°/2)) = 20.485 units

4. Perimeter Method

The perimeter of a circular segment is the total length of the arc and the chord.The formula for calculating the perimeter of acircular segmentis

Perimeter=Arc Length + Chord Length = 2πR * θ/360° + 2R * sin(θ/2)

Through conversion, the formula for calculating the radius can be obtained:

R = P/(2π * θ/360° + 2 * sin(θ/2))

Example: If the perimeter (P) is 15 units and the central angle (θ) is 120 degrees, the radius is:

R = P/(2π * θ/360° + 2 * sin(θ/2)) = 15/(2π * 120°/360° + 2 * sin(120°/2)) = 3.92 units

5. Area Method

If the area (A) and the central angle (θ) are known, the formula to find the radius of a circular segment is:

R = √(2A/(2π * θ/360° – sin(θ)))

Example: Given an area (A) of 20 square units and a central angle (θ) of 30 degrees, the radius is:

R = √(2A/(2π * θ/360 – sin(θ))) = √(2 * 20/(2π * 30°/360° – sin(30°))) = 41.17 units

FAQs:

Q: How does the Circular Segment Radius differ from the full circle radius?
A: The Circular Segment Radius specifically pertains to the radius of the curved portion between a chord and the circle arc, while the full circle radius is the radius of the entire circle.

Q: Is the formula applicable to all circular segments?
A: Yes, of course!

Q: Why is the circular segment radius important?
A: The radius is fundamental for applications in geometry, engineering, and design.

Q: Are these formulas universally applicable?
A: Yes, these formulas are versatile, applicable to various scenarios involving circular segments.

Q: How precise are the calculations?
A: The calculations are highly precise, keep 6 decimal places.

Q: Can I calculate the radius without knowing the central angle?
A: No. The central angle is a crucial parameter in these calculations. It’s recommended to have this information for accurate results.

Q: How does the calculator handle obtuse central angles?
A: The formulas are designed to accommodate obtuse central angles, ensuring accurate radius calculations.

Q: Can I use the calculator for 3D circular segments, such as in cylindrical shapes?
A: The calculator is primarily designed for 2D circular segments. For 3D applications, specialized formulas may be required.

Q: What units should I use for the input parameters?
A: The calculator is unit-agnostic, meaning you can use any consistent unit (e.g., inches, centimeters, etc.) for input parameters.

Q: How can I verify the accuracy of the calculated radius?
A: Cross-referencing with known geometric principles or using multiple methods to calculate the radius can help verify accuracy.For example, use the Circular Segment Calculator to verify.

Q: Are the calculations affected by the position of the circular segment within a larger shape?
A: No, the calculator is position-agnostic. It calculates the radius based on the provided parameters without considering the position.

Q: What if I encounter technical issues while using the calculator?
A: If you experience technical difficulties, ensure your browser is updated, and try clearing your cache. If issues persist, contact the support team.

Conclusion:

In conclusion, the Circular Segment Radius Calculator is a valuable companion in your geometric toolkit. Whether you’re working on architectural designs or simply exploring the beauty of circles, this calculator makes radius calculations a breeze.