Welcome to the world of curves and calculations with the Circular Segment Calculator! This tool is your key to unlocking the mysteries of circular segments, allowing you to effortlessly compute arc length, chord length, height, perimeter, and area.
Definition
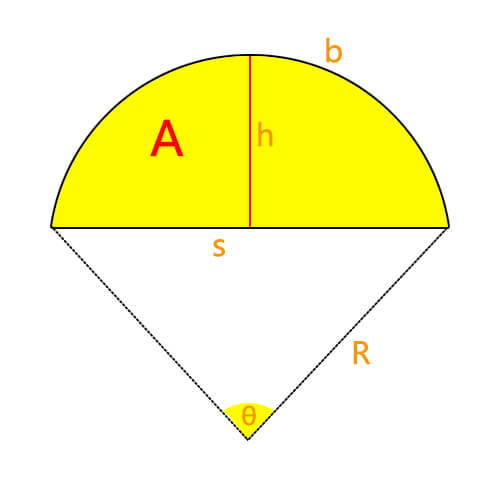
Circular Segment
A circular segment is the region enclosed by a chord and the arc subtended by that chord within a circle (The yellow part in the picture above).
Arc Length
The arc length is the measure of the curve along the circle’s circumference formed by a central angle (b in the picture).
Chord Length
The chord length is the straight-line distance between the endpoints of a circular segment (s).
Height of a Circular Segment
The height is the perpendicular distance between the chord and the center of the circle (h).
Perimeter of a Circular Segment
The perimeter is the total length of the arc and the chord (b + s).
Area of a Circular Segment
The area is the space enclosed by the circular segment, including the region under the arc and above the chord (A).
How to Calculate
Let’s embark on a journey through the step-by-step instructions for calculating various properties of a circular segment:
Calculating Arc Length
Identify the radius (R) and the central angle (θ).
Use the formula
Arc Length = θ/360° * 2πR
Example: For a circle with a radius of 10 units and a central angle of 60 degrees, the arc length is
Arc Length = θ/360° * 2πR = 60°/360° * 2π * 10 = 10.472 units
Calculating Chord Length
Identify the radius (R) and the central angle (θ).
Use the formula
Chord Length = 2R * sin(θ/2)
Example: With a radius of 12 units and a central angle of 45 degrees, the chord length is
Chord Length = 2R * sin(θ/2) = 2 * 12 * sin(45°/2) = 9.184 units
Calculating Height
Identify the radius (R) and the central angle (θ).
Use the formula
Height = R – R * cos(θ/2)
Example: If the radius is 15 units and a central angle of 90 degrees, the height is
Height = R – R * cos(θ/2) = 15 – 15 * cos(90°/2) = 4.393 units
Calculating Perimeter
Identify the radius (R) and the central angle (θ).
Use the formula
Perimeter = Arc Length + Chord Length = θ/360° * 2πR + 2R * sin(θ/2)
Example: If a circle with a radius of 10 units and a central angle of 60 degrees, the perimeter is
Perimeter = θ/360° * 2πR + 2R * sin(θ/2)
= 60°/360° * 2π * 10 + 2 * 10 * sin(60°/2)
= 20.472 units
Calculating Area
Identify the radius (R) and the central angle (θ).
Use the formula
Area= πR2 * θ/360° – 1/2 * R2 * sin(θ)
Example: With a radius of 15 units and a central angle of 60 degrees, the area is
Area = πR2 * θ/360° – 1/2 * R2 * sin(θ)
=π * 152 * 60°/360° – 1/2 * 152 * sin(60°)
= 20.382 square units
FAQs
- Q: Can I use the Circular Segment Calculator for any circle?A: Yes, the calculator is adaptable to circles of varying radii.
- Q: What happens if the central angle is 360 degrees?A: A central angle of 360 degrees corresponds to the entire circle, making the circular segment a full circle.
- Q: How precise are the results from the calculator?A: The calculator provides precise results, considering six decimal places for accuracy.
- Q: What if the chord length is greater than the circle's diameter?A: The chord length cannot exceed the circle’s diameter; otherwise, it would form a full circle.
- Q: Does the calculator support input in degrees and radians?A: Yes, you can input angles in degrees or radians based on your preference.
- Q: Is the height always equal to the radius?A: No, the height varies based on the central angle and chord length.
- Q: What applications benefit from calculating circular segment properties?A: Industries such as architecture, physics, and engineering use these calculations for diverse applications.
- Q: Are there restrictions on the values I can input for radius and angle?A: Input values should be positive and realistic within the context of circular segments.
Conclusion
Navigate the curves of circular segments with confidence using the Circular Segment Calculator. Calculate arcs, chords, heights, perimeters, and areas effortlessly, and embrace the elegance of circular geometry. Happy calculating!
Latest Calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Trigonometric Functions
Arccsc Calculator – Find the Exact Value of Inverse Cosecant
Arcsec Calculator – Find the Exact Value of Inverse Secant
Arccot Calculator – Find the Exact Value of Inverse Cotangent
Arctan Calculator – Find the Exact Value of Inverse Tangent
Inverse Cosine Calculator – Find The Exact Value of Arccos
Inverse Sine Calculator – Find The Exact Value of Arcsin
Inverse Trigonometric Functions Calculator
Trigonometric Functions Conversion Calculator
Trig Calculator – Find 6 Trigonometric Functions by Angles or Sides