Arctan Calculator is a simple tool for finding angles based on tangent values. All you have to do is enter the tangent value and get the corresponding angle in degrees or radians in the blink of an eye.
What is arctan?
The full name of arctan is arctangent, which is the inverse function of tangent. It is one of the six inverse trigonometric functions. In a right triangle, the arctangent is used to find the angle from the ratio of the opposite side to the adjacent side. In addition to arctan, the arctangent is also usually expressed in tan-1. Sometimes, you’ll see arctg, which used to be arctangent notation, but it’s outdated now.
Arctan graph and properties
Since tangent is a periodic function. In order to ensure that the tangent function has an inverse function, the domain of the tangent function is limited to (-π2, π2). According to the tangent graph, we can get the arctangent graph as follows
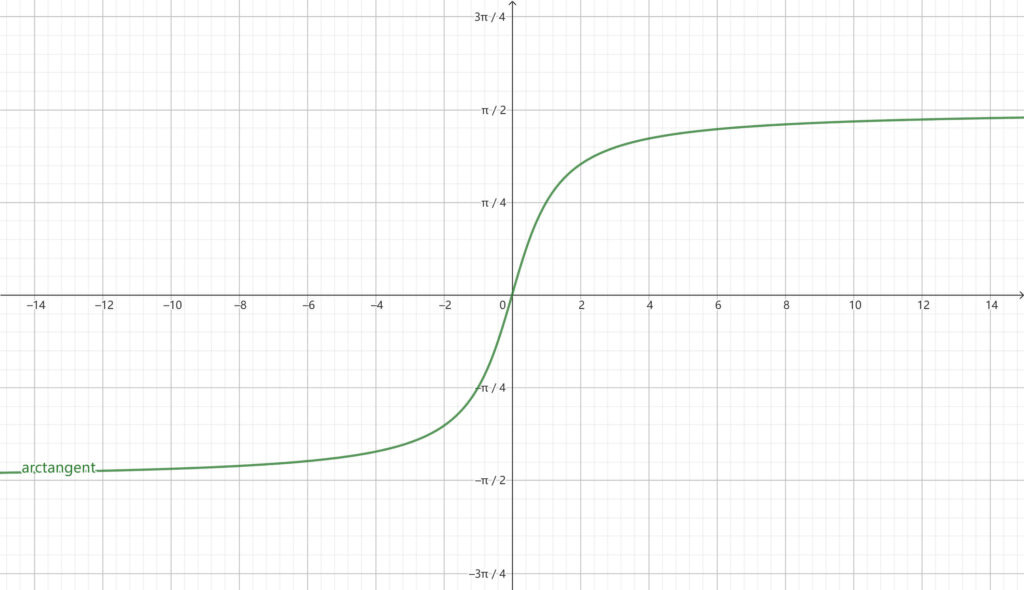
arctangent graph
- Domain – The domain of arctangent is all real numbers.
- Range – The arctangent is between -π2 and π2, excluding -π2 and π2.
- Monotonicity – In the domain, the arctangent is monotonically increasing
- Odd function – Since arctan(x) = -arctan(-x), the arctangent is an odd function.
How to calculate arctan?
There are two common ways to calculate the arctangent. One is to look up the table, and the other is to use a calculator. The look-up table is based on the inverse tangent table to find the relationship between the corresponding tangent value and the angle. The disadvantage of the inverse tangent table is that it cannot list all possible values. So, now everyone will borrow the arctan calculator to calculate the value of the inverse tangent function.
| arctan(x) | Degrees | Radians |
| -57.28996163 | -89° | -89π180 |
| -28.63625328 | -88° | -22π45 |
| -19.08113669 | -87° | -29π60 |
| -14.30066626 | -86° | -43π90 |
| -11.4300523 | -85° | -17π36 |
| -9.51436445 | -84° | -7π15 |
| -8.14434643 | -83° | -83π180 |
| -7.11536972 | -82° | -41π90 |
| -6.31375151 | -81° | -9π20 |
| -5.67128182 | -80° | -4π9 |
| -5.14455402 | -79° | -79π180 |
| -4.70463011 | -78° | -13π30 |
| -4.33147587 | -77° | -77π180 |
| -4.01078093 | -76° | -19π45 |
| -3.73205081 | -75° | -5π12 |
| -3.48741444 | -74° | -37π90 |
| -3.27085262 | -73° | -73π180 |
| -3.07768354 | -72° | -2π5 |
| -2.90421088 | -71° | -71π180 |
| -2.74747742 | -70° | -7π18 |
| -2.60508906 | -69° | -23π60 |
| -2.47508685 | -68° | -17π45 |
| -2.35585237 | -67° | -67π180 |
| -2.24603677 | -66° | -11π30 |
| -2.14450692 | -65° | -13π36 |
| -2.05030384 | -64° | -16π45 |
| -1.96261051 | -63° | -7π20 |
| -1.88072647 | -62° | -31π90 |
| -1.80404776 | -61° | -61π180 |
| -1.73205081 | -60° | -1π3 |
| -1.66427948 | -59° | -59π180 |
| -1.60033453 | -58° | -29π90 |
| -1.53986496 | -57° | -19π60 |
| -1.48256097 | -56° | -14π45 |
| -1.42814801 | -55° | -11π36 |
| -1.37638192 | -54° | -3π10 |
| -1.32704482 | -53° | -53π180 |
| -1.27994163 | -52° | -13π45 |
| -1.23489716 | -51° | -17π60 |
| -1.19175359 | -50° | -5π18 |
| -1.15036841 | -49° | -49π180 |
| -1.11061251 | -48° | -4π15 |
| -1.07236871 | -47° | -47π180 |
| -1.03553031 | -46° | -23π90 |
| -1 | -45° | -1π4 |
| -0.96568877 | -44° | -11π45 |
| -0.93251509 | -43° | -43π180 |
| -0.90040404 | -42° | -7π30 |
| -0.86928674 | -41° | -41π180 |
| -0.83909963 | -40° | -2π9 |
| -0.80978403 | -39° | -13π60 |
| -0.78128563 | -38° | -19π90 |
| -0.75355405 | -37° | -37π180 |
| -0.72654253 | -36° | -1π5 |
| -0.70020754 | -35° | -7π36 |
| -0.67450852 | -34° | -17π90 |
| -0.64940759 | -33° | -11π60 |
| -0.62486935 | -32° | -8π45 |
| -0.60086062 | -31° | -31π180 |
| -0.57735027 | -30° | -1π6 |
| -0.55430905 | -29° | -29π180 |
| -0.53170943 | -28° | -7π45 |
| -0.50952545 | -27° | -3π20 |
| -0.48773259 | -26° | -13π90 |
| -0.46630766 | -25° | -5π36 |
| -0.44522869 | -24° | -2π15 |
| -0.42447482 | -23° | -23π180 |
| -0.40402623 | -22° | -11π90 |
| -0.38386404 | -21° | -7π60 |
| -0.36397023 | -20° | -1π9 |
| -0.34432761 | -19° | -19π180 |
| -0.3249197 | -18° | -1π10 |
| -0.30573068 | -17° | -17π180 |
| -0.28674539 | -16° | -4π45 |
| -0.26794919 | -15° | -1π12 |
| -0.249328 | -14° | -7π90 |
| -0.23086819 | -13° | -13π180 |
| -0.21255656 | -12° | -1π15 |
| -0.19438031 | -11° | -11π180 |
| -0.17632698 | -10° | -1π18 |
| -0.15838444 | -9° | -1π20 |
| -0.14054083 | -8° | -2π45 |
| -0.12278456 | -7° | -7π180 |
| -0.10510424 | -6° | -1π30 |
| -0.08748866 | -5° | -1π36 |
| -0.06992681 | -4° | -1π45 |
| -0.05240778 | -3° | -1π60 |
| -0.03492077 | -2° | -1π90 |
| -0.01745506 | -1° | -1π180 |
| 0 | 0° | 0 |
| 0.01745506 | 1° | π180 |
| 0.03492077 | 2° | π90 |
| 0.05240778 | 3° | π60 |
| 0.06992681 | 4° | π45 |
| 0.08748866 | 5° | π36 |
| 0.10510424 | 6° | π30 |
| 0.12278456 | 7° | 7π180 |
| 0.14054083 | 8° | 2π45 |
| 0.15838444 | 9° | π20 |
| 0.17632698 | 10° | π18 |
| 0.19438031 | 11° | 11π180 |
| 0.21255656 | 12° | π15 |
| 0.23086819 | 13° | 13π180 |
| 0.249328 | 14° | 7π90 |
| 0.26794919 | 15° | π12 |
| 0.28674539 | 16° | 4π45 |
| 0.30573068 | 17° | 17π180 |
| 0.3249197 | 18° | π10 |
| 0.34432761 | 19° | 19π180 |
| 0.36397023 | 20° | π9 |
| 0.38386404 | 21° | 7π60 |
| 0.40402623 | 22° | 11π90 |
| 0.42447482 | 23° | 23π180 |
| 0.44522869 | 24° | 2π15 |
| 0.46630766 | 25° | 5π36 |
| 0.48773259 | 26° | 13π90 |
| 0.50952545 | 27° | 3π20 |
| 0.53170943 | 28° | 7π45 |
| 0.55430905 | 29° | 29π180 |
| 0.57735027 | 30° | π6 |
| 0.60086062 | 31° | 31π180 |
| 0.62486935 | 32° | 8π45 |
| 0.64940759 | 33° | 11π60 |
| 0.67450852 | 34° | 17π90 |
| 0.70020754 | 35° | 7π36 |
| 0.72654253 | 36° | π5 |
| 0.75355405 | 37° | 37π180 |
| 0.78128563 | 38° | 19π90 |
| 0.80978403 | 39° | 13π60 |
| 0.83909963 | 40° | 2π9 |
| 0.86928674 | 41° | 41π180 |
| 0.90040404 | 42° | 7π30 |
| 0.93251509 | 43° | 43π180 |
| 0.96568877 | 44° | 11π45 |
| 1 | 45° | π4 |
| 1.03553031 | 46° | 23π90 |
| 1.07236871 | 47° | 47π180 |
| 1.11061251 | 48° | 4π15 |
| 1.15036841 | 49° | 49π180 |
| 1.19175359 | 50° | 5π18 |
| 1.23489716 | 51° | 17π60 |
| 1.27994163 | 52° | 13π45 |
| 1.32704482 | 53° | 53π180 |
| 1.37638192 | 54° | 3π10 |
| 1.42814801 | 55° | 11π36 |
| 1.48256097 | 56° | 14π45 |
| 1.53986496 | 57° | 19π60 |
| 1.60033453 | 58° | 29π90 |
| 1.66427948 | 59° | 59π180 |
| 1.73205081 | 60° | π3 |
| 1.80404776 | 61° | 61π180 |
| 1.88072647 | 62° | 31π90 |
| 1.96261051 | 63° | 7π20 |
| 2.05030384 | 64° | 16π45 |
| 2.14450692 | 65° | 13π36 |
| 2.24603677 | 66° | 11π30 |
| 2.35585237 | 67° | 67π180 |
| 2.47508685 | 68° | 17π45 |
| 2.60508906 | 69° | 23π60 |
| 2.74747742 | 70° | 7π18 |
| 2.90421088 | 71° | 71π180 |
| 3.07768354 | 72° | 2π5 |
| 3.27085262 | 73° | 73π180 |
| 3.48741444 | 74° | 37π90 |
| 3.73205081 | 75° | 5π12 |
| 4.01078093 | 76° | 19π45 |
| 4.33147587 | 77° | 77π180 |
| 4.70463011 | 78° | 13π30 |
| 5.14455402 | 79° | 79π180 |
| 5.67128182 | 80° | 4π9 |
| 6.31375151 | 81° | 9π20 |
| 7.11536972 | 82° | 41π90 |
| 8.14434643 | 83° | 83π180 |
| 9.51436445 | 84° | 7π15 |
| 11.4300523 | 85° | 17π36 |
| 14.30066626 | 86° | 43π90 |
| 19.08113669 | 87° | 29π60 |
| 28.63625328 | 88° | 22π45 |
| 57.28996163 | 89° | 89π180 |
How to use this arctan calculator
The use of the arctan calculator is very simple, just enter the value and click the calculation button. This value can be an integer, decimal or fraction. The numerator and denominator of fractions are separated by /. For example, 3, 0.5, 1/4 and so on.
FAQS
- Q: Are arctan and tan^-1 the same?A: Yes, they both mean arctangent.
- Q: Is arctangent equal to cos/sin?
- Q: Are inverse tangent and cotangent the same?A: No. They are different. The inverse function of tangent is arctangent, and cotangent is the reciprocal of tangent.
- Q: What is the inverse tangent of tangent?A: Denote an angle as θ, then the inverse tangent of tangent is equal to θ.
arctan(tan(θ)) = θ
- Q: Is inverse tangent equal to adjacent over opposite?A: No. The inverse tangent is the angle obtained from the ratio of the opposite side to the adjacent side. And adjacent over opposite represents the cotangent. The two of them are completely different.
- Q: When to use inverse tangent?A: In a right triangle, when the ratio of the opposite side to the adjacent side of the acute angle is known, to calculate the angle, the arctangent can be considered.
Conclusion
In short, the arctangent is defined as an angle, which is the inverse function of the tangent. If you want to calculate the value of the arctangent, please use the arctan calculator provided on this page.
Latest Calculators
Standard Form to Slope-Intercept Form Calculator
Slope Intercept Form Calculator
Slope Calculator: Calculate Slope, X-Intercept, Y-Intercept
Reciprocal of Complex Number Calculator
Conjugate Complex Number Calculator
Modulus of Complex Number Calculator
Profit Percentage Calculator: Calculate Your Profitability Easily
Attendance and Absence Percentage Calculator
Trigonometric Functions
Arccsc Calculator – Find the Exact Value of Inverse Cosecant
Arcsec Calculator – Find the Exact Value of Inverse Secant
Arccot Calculator – Find the Exact Value of Inverse Cotangent
Inverse Cosine Calculator – Find The Exact Value of Arccos
Inverse Sine Calculator – Find The Exact Value of Arcsin
Inverse Trigonometric Functions Calculator
Trigonometric Functions Conversion Calculator
Trig Calculator – Find 6 Trigonometric Functions by Angles or Sides