Online Antilog Calculator - Inverse Logarithm

This antilog calculator is a free online tool to find the value of the inverse logarithm. The base and logarithm of the antilog can be entered freely.

Antilog Calculator

antilog_ab = ?

Eg, What is the inverse log of 6 base 2? Enter 2 in the first input box and enter 6 in the second input box, then click Calculate button.

Calculate Reset

What is antilog? - Relation between exponent, log, and antilog

Let’s start with logarithms. If a raised to the b power is equal to x (exponentiation a^b = x), then the number x is called the logarithm of b to the base a. Denoted as

log_ab = x

Among them, a is called the base number, b is a real number, and x is a logarithm. The logarithmic calculation is to find the logarithm when the base and real number are known (Given a and b, compute x). This is also the inverse operation of exponentiation.

The antilog is the inverse of the logarithmic function. That is, finds the real number given the base and logarithm (a and x are known, calculate b). The expression for the antilog is antilog_ax or log^-1_ax. Usually, if the base is not given, it defaults to 10.

Since the logarithm is the inverse function of exponentiation, and the antilogarithm is the inverse function of the logarithm. So, the antilog is the same as the exponent.

antilog_ax = a^x

How to calculate antilog? - Manual and Calculator

Since the antilog is the same as the exponent, computing the antilog is the process of exponentiation.

For example, find the antilog of 3 with a base of 4.

Here, the base is 4 and the exponent is 3.

So, the antilog of 3 with a base of 4 is

antilog₄3 = 4³ = 4 * 4 * 4 = 64

This is the simpler case, where both base and exponent are integers. If you encounter complex situations, such as decimals, etc., you can use the antilog calculator we provided above, or use a scientific calculator.

How to find the antilog in a scientific calculator?

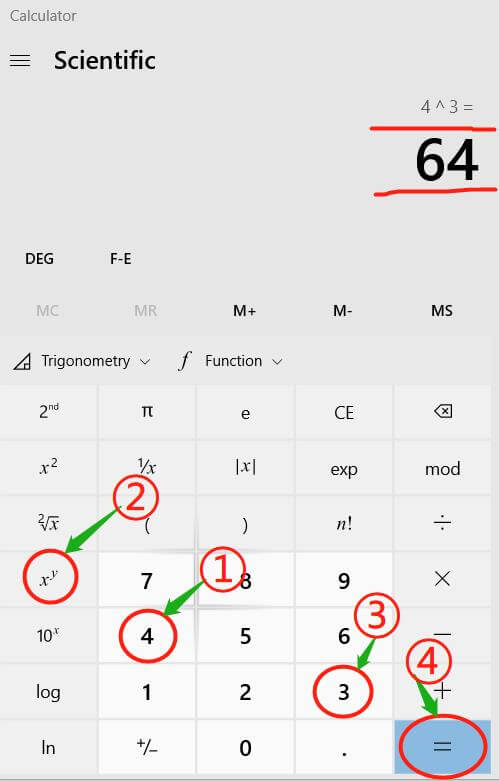
First, figure out the base and exponent. In the example above, the base is 4 and the exponent is 3.

Then open the scientific calculator, enter the base 4.

Third, press the x^y button.

Fourth, enter the exponent, here is 3.

Finally, press the equal button to get the result.

The antilog for the base 4 of 3 is also 64.

find antilog in scientific calculator

How to use this antilog calculator

The Antilog Calculator is very simple to use. Enter the base first, then the logarithm, and finally click Calculate. Notice, the base and logarithm are not only integers, but also decimals or fractions. If the base is not entered, it defaults to 10.

FAQS

Q: What is an Antilog Calculator?
A: The antilog calculator is a calculator specially used to calculate the antilog value.

Q: Can negative numbers be entered?
A: Yes, of course.

Q: Can the value of the antilog be negative?
A: Yes, it is possible. As with exponents, it depends on the base. If the base is negative, the result may also be negative. If the base is positive, then the antilog value must be positive.

Q: What is the antilog button on a calculator? How to calculate?
A: The antilog button on the calculator is x^y. The premise is to replace the calculator with a scientific calculator first. Then, enter the base, press the x^y button, next enter the logarithm, and finally press the = button. The antilog value will appear on the screen.

Q: How to enter the base of natural logarithm?
A: Just enter the English letter e.

Conclusion

In summary, the antilog is the inverse of the log, the same as exponentiation. If you want to calculate the antilog value, follow the steps for exponentiation. Or use the Antilog Calculator provided on this page. This calculator is convenient and fast, there is no threshold for use, and the most important thing is that it is free. Why not try it?