Almost Perfect Number Checker

Check if the given number is an Almost Perfect Number.

Welcome to the Almost Perfect Number Checker! In this article, we’ll dive into the concept of almost perfect numbers and provide step-by-step instructions on how to check for almost perfect numbers, and showcase solved examples. Let’s embark on this mathematical journey together!

Almost Perfect Number Checker

Eg, Is 32 an almost perfect number? Enter 32 into the input box and click Check button.

Check Reset

What is Almost Perfect Number

Almost perfect numbers are intriguing mathematical entities that possess a unique property. An almost perfect number is a positive integer where the sum of its proper divisors (excluding the number itself) is equal to one less than the number itself. In other words, an almost perfect number is the result of the sum of factors excluding the number itself being one less than the number.

The key distinction between almost perfect numbers and perfect numbers lies in the condition they satisfy. Perfect numbers have the sum of proper divisors equal to the number itself, while almost perfect numbers have the sum either greater than or less than the number by 1.

By understanding this distinction, we can differentiate between perfect and almost perfect numbers and apply the appropriate criteria when checking for almost perfectness.

How to Check for Almost Perfect Numbers

To check whether a number is almost perfect, follow these steps:

Identify the number for which you want to determine its almost perfect nature.
Calculate the sum of its proper divisors (divisors excluding the number itself).
Compare the sum with one less than the number itself.
If the two values match, the number is almost perfect. Otherwise, it is not.

Let’s check whether the number 32 is almost perfect.

Step 1: Identify the number: 32

Step 2: Calculate the sum of its proper divisors: The proper divisors of 32 are 1, 2, 4, 8, and 16. Their sum is 1 + 2 + 4 + 8 + 16 = 31.

Step 3: Compare the sum with one less than the number itself: 32 – 1 = 31.

Step 4: The sum (32) is equal to one less than the number itself (31).

So, the number 32 is almost perfect.

In this example, we observe that the sum of the proper divisors of 32 equals one less than the number itself, fulfilling the criteria of an almost perfect number.

Remember, you can apply the same steps to any number you wish to check for almost perfectness.

What is an Almost Perfect Number Checker

The Almost Perfect Number Checker is a handy tool designed to quickly determine whether a given number is almost perfect. Its purpose is to simplify the process of verifying the almost perfect property of a number without manual calculations.

How to Use the Almost Perfect Number Checker

Using the Almost Perfect Number Checker is straightforward:

1Input the number you want to check.
2Click the Check button to initiate the verification process.
3Click the Reset button to start a new verification.

The result will indicate whether the number is almost perfect or not.

Solved Examples with the Checker

Let’s explore some solved examples using the Almost Perfect Number Checker:

Example 1:

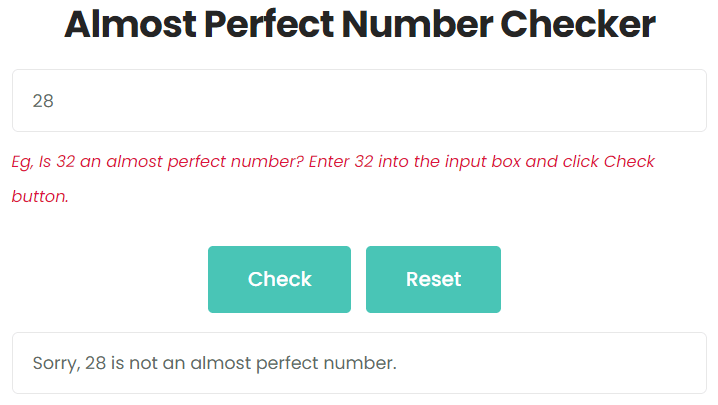
Is 28 an Almost Perfect Number?

Enter 28 into the input box and click Check button. As shown in the figure, 28 is not an almost perfect number.

Example 2:

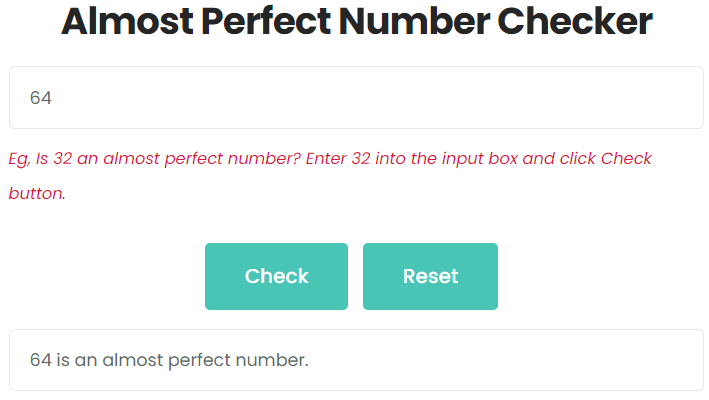
Is 64 an Almost Perfect Number?

Enter 64 into the input box and click Check button. As shown in the figure, 64 is an almost perfect number.

FAQS

Q1: What are proper divisors?
A: Proper divisors of a number are all the divisors excluding the number itself.

Q2: Are almost perfect numbers rare?
A: Yes, almost perfect numbers are relatively rare and challenging to find. The list of known almost perfect numbers is limited.

Q3: Can almost perfect numbers be negative?
A: No, almost perfect numbers are defined as positive integers.

Q4: Can an almost perfect number be an odd number?
A: No, almost perfect numbers are always even. This is because the sum of divisors for an odd number will always be greater than the number itself by at least 1.

Q5: Can an almost perfect number be a prime number?
A: No, almost perfect numbers cannot be prime numbers. Prime numbers have only two divisors: 1 and the number itself. Hence, their sum of proper divisors is always 1, which does not satisfy the condition for an almost perfect number.

Conclusion

Almost perfect numbers unveil the beauty and intricacy of number theory. Through this article, we’ve explored the definition of almost perfect numbers, learned how to check for their existence using the Almost Perfect Number Checker, and examined examples for a better understanding. Whether you’re an aspiring mathematician or someone seeking to expand their knowledge, delving into the realm of almost perfect numbers is a rewarding experience. So go ahead, explore the wonders of numbers, and unravel the secrets they hold!