Absolute Difference Calculator

Use the Absolute Difference Calculator to find the absolute value of the difference between two numbers. These two numbers can be integers, decimals, or fractions.

Absolute Difference Calculator

|a - b| = ?

Eg, What is the absolute difference between -4 and 6? Enter -4 in the first input box and enter 6 in the second input box, then click Calculate button.

Calculate Reset

What is the absolute difference?

As the name suggests, the absolute difference represents the absolute value of the difference between two numbers. Placed on a number line to represent the distance between two points. For instance, the distance between a and b on the number axis is represented by the absolute difference |a-b|.

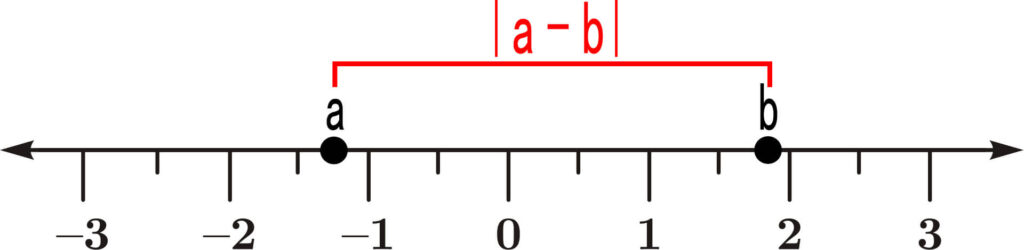absolute difference If one of the points is the origin, it is expressed as an absolute value. Such as, |a – 0| = |a|.

How to find the absolute difference?

From the above definition, it is clear that calculating the absolute difference requires two steps.

Find the difference between two numbers.
Calculate the absolute value of the difference.

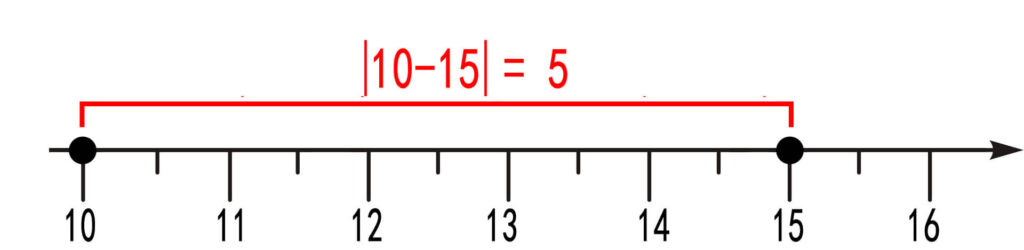
For example, what is the absolute difference between 10 and 15?

First, find the difference between 10 and 15.

10 – 15 = -5

Second, calculate the absolute value of -5.

|-5| = 5

So, the absolute difference between 10 and 15 is 5. This means that the distance from 10 to 15 on the number line is 5.

absolute difference between 10 and 15 Note that the order of the two numbers does not matter when calculating the difference. As shown in the example above, swapping the positions of two numbers yields the same answer.

|10 – 15| = |-5| = 5

|15 – 10| = |5| = 5

How to use the absolute difference calculator

To use the absolute difference calculator, simply enter numbers into the two input boxes and click Calculate. The absolute difference between them will come out immediately. Don’t worry about the order of the two numbers, it doesn’t affect the final result. Just let go of input.

FAQS

Q: Can absolute difference be negative?
A: No. The absolute difference between two numbers is a positive number. Just like absolute value.
Q: Can I enter decimals or fractions?
A: Of course, it’s perfectly fine.
Q: How can I use the absolute difference calculator? Does it have to do with the order of the numbers?
A: It doesn’t matter the order of the numbers, just enter two numbers and click calculate.
Q: Is the absolute difference the same as the difference in absolute value?
A: Quite different. The former calculates the absolute value after calculating the difference, and the result is a positive number. The latter is to calculate the absolute value first, and then calculate the difference.

For example, find the absolute difference between -2 and 3.

|(-2) – 3| = |-5| = 5

The difference between absolute values -2 and 3 is

|-2| – |3| = 2 – 3 = -1

Obviously, the two answers are different.
Q: Do I need to register or pay a fee before using the Absolute Value Calculator?
A: 100% guaranteed, no login required, unlimited times and free for life.

Conclusion

The absolute difference is a very common calculation, it is a mixture of difference and absolute value. To avoid mistakes, we recommend using our absolute difference calculator, which is efficient and free. Try it once and you’ll love it.

Back to top of page